線形と非線形の違いとは？未来予測が容易で安定して稼げるビジネスの作り方

今すぐ無料体験してみる

前回の記事更新から早4カ月。
このままではいけない！と思い記事を書いています。どうもちらです！( ｀ー´)ノ

今回の記事の目的は、数学や物理で出てくる、”線形と非線形の違い”を理解し、
”未来予測が容易で安定して稼げるビジネスモデルを作るための考え方”を身に着けることです。

線形と非線形・・・
これら二つの言葉を理解することで安定した収益をもたらす
ビジネスモデルを考える際にとても役立つ思考が可能になります。

では、まずは線形と非線形について説明していきますね。
一応、数式＆日本語訳両方を使って説明しますが、
こんがらがってわからない人はとりあえず最初の数行だけわかればOKです笑
そのあと具体例を出して説明していくので^^

線形と非線形ってなあに？ざっくり説明と数式説明で理解！
線形世界は未来予測＆コントロールが簡単な世界　具体例で理解しよう！
安定して稼ぐなら線形的なビジネスモデルを作りたい・・・が？
1. 線形化とは
まとめ

線形と非線形ってなあに？ざっくり説明と数式説明で理解！

”線形”という概念の説明から始めます。

まずは漢字の意味を考えてみましょう。
読んで字のごとく、線形とは、直線的な形をしている。つまり、比例関係を意味しています。
中学時代の数学で言うと、y=2xというような直線式を線形といいます。
”線状になっていれば線形”、感覚的にはこれでOKです(*’ω’*)

直線なら線形！直線じゃなければ非線形！

数式を利用した正確な線形性の定義としては、二つの式があります。

f(x+y) = f(x) + f(y)
k×f(x) = f(kx)

これら二つの式を満たす性質を持つと”線形である”といいます。
はい、おわり！(*’▽’)

（　＾ω＾）・・・

( ;∀;)・・・

え？式はよくわからないって？(;’∀’)

わ、わかりました。

であれば、これら二つの式を翻訳してみましょう。
翻訳する式は、

f(x+y) = f(x) + f(y)
k×f(x) = f(kx)

数式を日本語訳すると、
f(x)のf()は()内の数値を処理する何らかのシステム(関数)、
f(x)の中のxは入力値を意味しています。

入力値x+yをシステムfに与えたときに出てくる出力値は
入力値xをシステムfに与えたときの出力値と、入力値yをシステムfに与えた出力値の足し算に等しい(重ね合わせの法則)
入力値xをシステムfに与えたときの出力値をk倍したものと、
入力値をk倍したkxをシステムfに与えたときの出力値は等しい。

という翻訳になります。

ようするに、あるシステムの中に入力値を分けて入れても、一度に入れても結果は変わらない。
そして、値を入力して結果をk倍しても、入力値をk倍してシステムに入れても、結果は変わらない。

ということです(*’ω’*)

逆に、これらの性質を満たさないシステムのことを”非線形”と呼びます。

ここまで読んでわからない・・・そう思った人はやはりざっくりこう考えましょう。

・グラフを描いたときに直線になってれば線形！

・グラフを描いたときに直線になってなければ非線形！

で、こうした線形と非線形という概念を理解するとビジネスがとてもやりやすくなります(*’ω’*)
次に、ビジネスやアフィリエイトで線形や非線形の考え方をどう適用するか書いていきます(追記：アフィリエイトへの適用は次回になります)。

線形世界は未来予測＆コントロールが簡単な世界　具体例で理解しよう！

線形、つまり直線式って先を予測しやすいですよね。

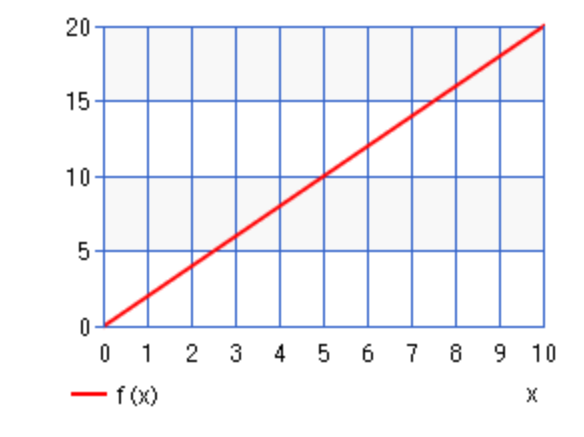
例えば、こんなグラフ。y=2xのグラフです。
この図ではx=0から10の範囲しか描いていませんが、
x=20のときの値を答えなさいって言われたら答えられますよね？
まあ、普通なら40って答えますよね(*’ω’*)

線形の世界は未来予測がとても容易です。
この図の横軸が時間で単位を年、縦軸が1年あたりの売り上げで単位を100万としてみると、
0年目には0円だった売り上げが、1年後には200万、10年後には20×100万で2000万の売り上げに成長する。
そんな風に読むことができます。
20年後ではどうでしょうか？
そう、4000万円ですね。

こういった形で売り上げが伸びていくビジネスを持っていれば、
そのビジネスは線形的なビジネスであると言えます。

つまり、未来の売り上げ、成長が予測しやすいビジネスモデルです。

まあ、ずーーーっと永遠にこんな感じで線形的になるビジネスなんて作れないと思いますけどね(‘ω’)ノ←
でも、ある程度の時間幅であれば構築可能でしょう( ｀ー´)ノ

では、別のパターンも見てみましょう。

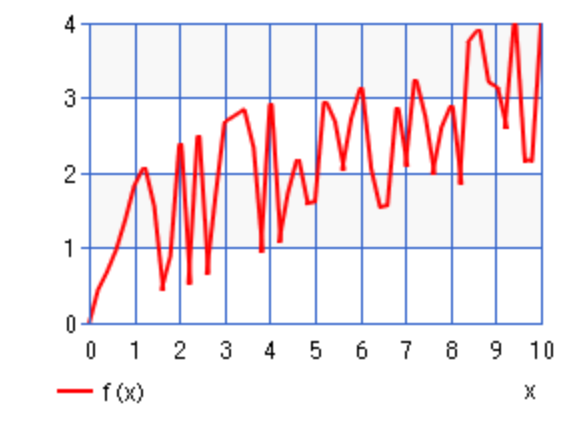
はい！(*’▽’)

こちら、y=√(x)+sin(x^3)になります。
これが非線形なシステムです。
先ほど述べた線形の性質を満たさない式になります。
もう見ての通り、ぐちゃぐちゃですね汗

ちゃんと先に数式を出されていればxに値を代入することでどんなyでも求められます(未来の売り上げがわかります)が、
いきなりこのグラフだけ見てx=20の20年後の売り上げを予測できる人はいないと思います( ｀ー´)ノ

これ、売り上げがうまく伸び切らないビジネスでありそうな形ですよねｗ
もしあなたのビジネスがこんな風になってたらちょっと嫌ですよね。。。

売り上げが上がったり下がったりして、しかも数年後にどうなるか予測しづらい。
つまり、どれだけそのビジネスにリソースをかけていいか、ほかのビジネスをやるべきかがわかりづらい・・・

こういったビジネスモデルは非線形なビジネスといえます。

つまり、未来の売り上げ、成長が予測しづらいビジネスモデルです。

線形と非線形の違い、わかってきましたか？

直線的な挙動を見せるグラフが線形、非直線的なグラフが非線形。
そして、線形的な性質を持つビジネスモデルを作れると未来予測が容易になることがわかります。

もう一つ、こんなグラフも非線形の仲間です。

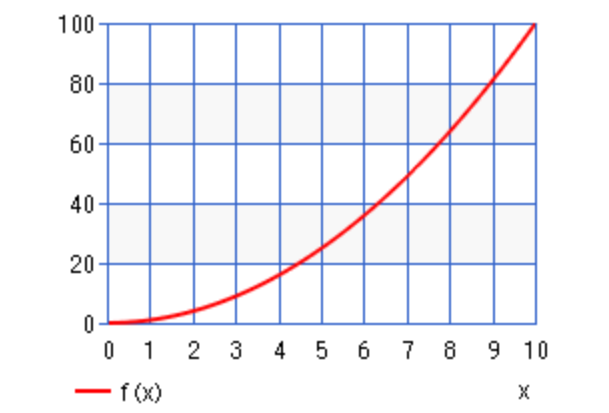
おお・・・(*’ω’*)

こんな売り上げの伸び方をするビジネスモデル、欲しいですね笑
ちなみにこちらはy=x^2のグラフです。
1年後の売り上げが100万、2年後は400万・・・そして10年後の売り上げが1億(‘_’)

初年度だけ見るとy=2xのグラフよりも売り上げが低いですが、10年後になるととんでもないことになっています。
ここまで綺麗なグラフだと未来予測もできそうですし、理想的な売り上げの伸び方ですね。
かなり非現実的ではありますが・・・こんなビジネス作れるなら非線形万歳ですね(*’▽’)

安定して稼ぐなら線形的なビジネスモデルを作りたい・・・が？

さて、ここまでの内容から、

・線形＝直線的＝未来予測が容易
・非線形＝非直線的＝未来予測が困難

ということがわかりました。

安定して稼ぎたいなら線形的なビジネスモデル、
先が読みづらいが大きく稼ぐ可能性を狙うなら非線形的なビジネスモデルの構築を目指すのがいいでしょう。

「僕は線形的で安定して売り上げが出るビジネスモデルがいい！」
「私は大きく発展する可能性がある非線形的なビジネスモデルがいいわ！」

などと思うかもしれません(‘ω’)ノ

ですが、はい、お察しの通り。
具体的にどうやって望みのビジネスモデルを作るのか。
ここを考えなくてはいけません。

人間社会は基本的に強非線形性の世界(株価・為替・経済指標などのグラフを見てみれば線形的な性質などほぼ見当たりません)。
無計画にビジネスを初めても、売り上げを安定化させ、
コントロールしやすいビジネスを構築することは非常に困難です。

超お金持ちになりたい人やギャンブラー気質の人は
未来なんて読めない、先なんてわからない世界に飛び込むのもいいでしょう。
ですが、ちらの場合(あなたもそうかもしれないですが)は

”再起不能にならずに、
自分の好きな活動を好きにやるために安定し、
コントロールしやすいビジネスモデルを作りたい”

と考えていました。

そこで、ちらは
「どうしたら線形的なビジネスモデルを強非線形の人間社会から取り出して作ればいいのか」
ということを考えました。
強非線形の人間社会から線形的な自分のビジネスを組み立てたい。そんな解法はないだろうかと。

それがあるんですね。
物理の世界ではこのような方策を”線形化”と呼びます。

線形化とは

“線形化” とは、操作点の周りの小さい領域で有効な非線形システムの線形近似です。

たとえば、非線形関数が y=x^2 であるとします。操作点 x = 1、y = 1 に関してこの非線形関数を線形化すると、線形関数 y=2x−1 が得られます。

操作点の近くでは、y=2x−1 は y=x^2 をよく近似しています。操作点から離れると、近似度は低くなります。

次の図は、y=x^2 の線形化への近似度が高いと考えられる領域を示しています。実際の有効領域は、非線形モデルによって異なります。

(引用元：https://jp.mathworks.com/help/slcontrol/ug/linearizing-nonlinear-models.html)